Advanced R¶

Introduction¶

In this lecture, we will talk about efficient computation in R.

R is a vector-oriented language. In most cases, vectorization speeds up computation.
We turn to more CPUs for parallel execution to save time if there is no more room to optimize the code to improve the speed.
Servers are accessed remotely. Communicating with a remote cluster is different from operating a local machine.

Vectorization¶

Despite mathematical equivalence, various ways of calculation can perform distinctively in terms of computational speed.

Does computational speed matter? For a job that takes less than a minutes, the time difference is not a big deal. But sometimes economic problems can be clumsy. For structural estimation commonly seen in industrial organization, a single estimation can take up to a week. In econometrics, other computational intensive procedures include bootstrap, simulated maximum likelihood and simulated method of moments. Even if a single execution does not take much time, repeating such a procedure for thousands of replications will consume a non-trivial duration. Moreover, machine learning methods that crunch big data usually involve tuning parameters, so the same procedure must be carried out at each point of a grid of tuning parameters. For example, the preferred algorithm in @lin2020 takes 8 hours on a 24-core remote server to find out the best combination of tuning parameters. For those problems, code optimization is essential.

Of course, optimizing code takes human time. It is a balance of human time and machine time.

Example

In OLS regression, under homoskedasticity

\[ \sqrt{n}\left(\widehat{\beta}-\beta_{0}\right)\stackrel{d}{\to}N\left(0,\sigma^{2}\left(E\left[x_{i}x_{i}'\right]\right)^{-1}\right) \]

where the asymptotic variance can be consistently estimated by $(X'X)^{-1} \sum_{i=1}^n \widehat{e}^{2}$. However, under heteroskedasticity

\[ \sqrt{n}\left(\widehat{\beta}-\beta_{0}\right)\stackrel{d}{\to}N\left(0,E\left[x_{i}x_{i}'\right]^{-1}\mathrm{var}\left(x_{i}e_{i}\right)E\left[x_{i}x_{i}'\right]^{-1}\right) \]

where $\mathrm{var}\left(x_{i}e_{i}\right)$ can be estimated by

\[ \underset{\mathrm{opt1}}{\frac{1}{n}\sum_{i=1}^{n}x_{i}x_{i}'\widehat{e}_{i}^{2}}=\underset{\mathrm{opt2,3}}{\frac{1}{n}X'DX}=\underset{\mathrm{opt 4}}{\frac{1}{n}\left(X'D^{1/2}\right)\left(D^{1/2}X\right)} \]

where $D$ is a diagonal matrix of $\left(\widehat{\epsilon}_{1}^{2},\widehat{\epsilon}_{2,}^{2},\ldots,\widehat{\epsilon}_{n}^{2}\right)$. There are at least 4 mathematically equivalent ways to compute the “meat” of the sandwich form.

literally sum $\hat{e}_i^2 x_i x_i'$ over $i=1,\ldots,n$ one by one.
$X' \mathrm{diag}(\hat{e}^2) X$, with a dense central matrix.
$X' \mathrm{diag}(\hat{e}^2) X$, with a sparse central matrix.
Do cross product to X*e_hat. It takes advantage of the element-by-element operation in R.

We first generate the data of binary response and regressors. Due to the discrete nature of the dependent variable, the error term in the linear probability model is heteroskedastic. It is necessary to use the heteroskedastic-robust variance to consistently estimate the asymptotic variance of the OLS estimator. The code chunk below estimates the coefficients and obtains the residual.

# an example of robust variance matrix.
# compare the implementation via matrix, Matrix (package) and vecteroization.

# n = 5000; Rep = 10; # Matrix is quick, matrix is slow, adding is OK

source("data_example/lec2.R")

n <- 50
Rep <- 1000 

data.Xe <- lpm(n) # see the function in "data_example/lec2.R"
X <- data.Xe$X
e_hat <- data.Xe$e_hat

XXe2 <- matrix(0, nrow = 2, ncol = 2)

We run the 4 estimators for the same data, and compare the time.

for (opt in 1:4) {
  pts0 <- Sys.time()

  for (iter in 1:Rep) {
    set.seed(iter) # to make sure that the data used
    # different estimation methods are the same


    if (opt == 1) {
      for (i in 1:n) {
        XXe2 <- XXe2 + e_hat[i]^2 * X[i, ] %*% t(X[i, ])
      }
    } else if (opt == 2) { # the vectorized version with dense matrix
      e_hat2_M <- matrix(0, nrow = n, ncol = n)
      diag(e_hat2_M) <- e_hat^2
      XXe2 <- t(X) %*% e_hat2_M %*% X
    } else if (opt == 3) { # the vectorized version with sparse matrix
      e_hat2_M <- Matrix::Matrix(0, ncol = n, nrow = n)
      diag(e_hat2_M) <- e_hat^2
      XXe2 <- t(X) %*% e_hat2_M %*% X
    } else if (opt == 4) { # the best vectorization method. No waste
      Xe <- X * e_hat
      XXe2 <- t(Xe) %*% Xe
    }


    XX_inv <- solve(t(X) %*% X)
    sig_B <- XX_inv %*% XXe2 %*% XX_inv
  }
  cat("n =", n, ", Rep =", Rep, ", opt =", opt, ", time =", Sys.time() - pts0, "\n")
}

We clearly see the difference in running time, though the 4 methods are mathematically the same. When $n$ is small, matrix is fast and Matrix is slow; the vectorized version is the fastest. When $n$ is big, matrix is slow and Matrix is fast; the vectorized version is still the fastest.

In this simulation exercise, we repeat the procedure many times to make the time comparison more evident, for a single execution takes very short time in this simple operation. A real-data example is in data_example/IPUMS.R with 234 thousand observations, where the time difference is dramatic but the intuitive solution indeed does not take much time. It demonstrates the usefulness of vectorization. Vectorization can significantly saves computing time in more complicated operations, for example, in heteroskedastic and autocorrelation consistent variance estimation (HAC) in econometrics which involves many layers of matrices.

Efficient Loop¶

R was the heir of S, an old language. R evolves with packages that are designed to adapt to new big data environment. Many examples can be found in @wickham2016r. Here we introduce plyr.

In standard for loops, we have to do a lot of housekeeping work. Hadley Wickham’s plyr simplifies the job and facilitates parallelization.

Example

Here we calculate the empirical coverage probability of a Poisson distribution of degrees of freedom 2. We first write a user-defined function CI for confidence interval, which was used in the last lecture.

This is a standard for loop.

Rep <- 100000
sample_size <- 1000
mu <- 2

source("data_example/lec2.R")
# append a new outcome after each loop
pts0 <- Sys.time() # check time
for (i in 1:Rep) {
  x <- rpois(sample_size, mu)
  bounds <- CI(x)
  out_i <- ((bounds$lower <= mu) & (mu <= bounds$upper))
  if (i == 1) {
    out <- out_i
  } else {
    out <- c(out, out_i)
  }
}

pts1 <- Sys.time() - pts0 # check time elapse
cat("loop without pre-definition takes", pts1, "seconds\n")


# pre-define a container
out <- rep(0, Rep)
pts0 <- Sys.time() # check time
for (i in 1:Rep) {
  x <- rpois(sample_size, mu)
  bounds <- CI(x)
  out[i] <- ((bounds$lower <= mu) & (mu <= bounds$upper))
}

pts1 <- Sys.time() - pts0 # check time elapse
cat("loop with pre-definition takes", pts1, "seconds\n")

Pay attention to the line out = rep(0, Rep). It pre-defines a vector out to be filled by out[i] = ( ( bounds$lower <= mu ) & (mu <= bounds$upper) ). The computer opens a continuous patch of memory for the vector out. When new result comes in, the old element is replaced. If we do not pre-define out but append one more element in each loop, the length of out will change in each replication and every time a new patch of memory will be assigned to store it. The latter approach will spend much more time just to locate the vector in the memory.

out is the result container. In a for loop, we pre-define a container, and replace the elements of the container in each loop by explicitly calling the index.

In contrast, a plyr loop saves the house keeping chores, and makes it easier to parallelize. In the example below, we encapsulate the chunk in the for loop as a new function capture, and run the replication via __ply. __ply is a family of functions. ldply here means that the input is a list (l) and the output is a data frame (d) .

library(plyr)

capture <- function(i) {
  x <- rpois(sample_size, mu)
  bounds <- CI(x)
  return((bounds$lower <= mu) & (mu <= bounds$upper))
}

pts0 <- Sys.time() # check time
out <- ldply(.data = 1:Rep, .fun = capture)

pts1 <- Sys.time() - pts0 # check time elapse
cat("plyr loop takes", pts1, "seconds\n")

This example is so simple that the advantage of plyr is not dramatic. The difference in coding will be noticeable in complex problems with big data frames. In terms of speed, plyr does not run much faster than a for loop. They are of similar performance. Parallel computing will be our next topic. It is quite easy to implement parallel execution with plyr—we just need to change one argument in the function.

Parallel Computing¶

Parallel computing becomes essential when the data size is beyond the storage of a single computer, for example @li2018embracing. Here we explore the speed gain of parallel computing on a multicore machine.

Here we introduce how to coordinate multiple cores on a single computer. The packages foreach and doParallel are useful for parallel computing. Below is the basic structure. registerDoParallel(number) prepares a few CPU cores to accept incoming jobs.

library(plyr); library(foreach); library(doParallel)

registerDoParallel(a_number) # opens specified number of CPUs

out <- foreach(icount(Rep), .combine = option) %dopar% {
  my_expressions
}

If we have two CPUs running simultaneously, in theory we can cut the time to a half of that on a single CPU. Is that what happening in practice?

Example

Compare the speed of a parallel loop and a single-core sequential loop.

library(foreach)
library(doParallel)

registerDoParallel(2) # open 2 CPUs

pts0 <- Sys.time() # check time

out <- foreach(icount(Rep), .combine = c) %dopar% {
  capture()
}

pts1 <- Sys.time() - pts0 # check time elapse
cat("parallel loop takes", pts1, "seconds\n")

Surprisingly, the above code block of parallel computing runs even more slowly. It is because the task in each loop can be done in very short time. In contrast, the code chunk below will tell a different story. There the time in each loop is non-trivial, and then parallelism dominates the overhead of the CPU communication. The only difference between the two implementations below is that the first uses %dopar% and the latter uses %do%.

Rep <- 200
sample_size <- 2000000

registerDoParallel(8) # change the number of open CPUs according to
# the specification of your computer

pts0 <- Sys.time() # check time
out <- foreach(icount(Rep), .combine = c) %dopar% {
  capture()
}

cat("8-core parallel loop takes", Sys.time() - pts0 , "seconds\n")

pts0 <- Sys.time()
out <- foreach(icount(Rep), .combine = c) %do% {
  capture()
}

cat("single-core loop takes", Sys.time() - pts0 , "seconds\n")

Cloud Computing¶

Investing money from our own pocket to an extremely powerful laptop to conduct heavy-lifting computational work is unnecessary. (i) We do not run these long jobs every day, it is more cost efficient to share a workhorse. (ii) We cannot keep our laptop always on when we move it around. The right solution is cloud computing on a server.

Many of us have experience with cloud storage, such as Dropbox and Baidu Netdisk. Few people are exposed to cloud computing. However, no fundamental difference lies between local and cloud computing. We prepare in the cloud serve the data and code, open a shell for communication, run the code, and collect the results. One potential obstacle is dealing with a command-line-based operation system. Such command line tools is the norm of life two or three decades ago, but today we mostly work in a graphic operating system like Windows or OSX. For Windows users (I am one of them), I recommend Git Bash as a shell, and WinSCP, a graphic interface for input and output.

Cloud computing also provides a strong justification for open-source languages such as R or Python. These open-source languages can be installed on as many remote serves as the resource permits. In contrast, proprietary software will be prohibitively expensive for server licensing.

Command Line¶

Most servers run Unix/Linux operation system. Here are a few commands for basic operations.

mkdir: make directory
cd: change directory
copy: copy files
top: check login status
screen: a separated screen for isolation
ssh: user@address
start a program

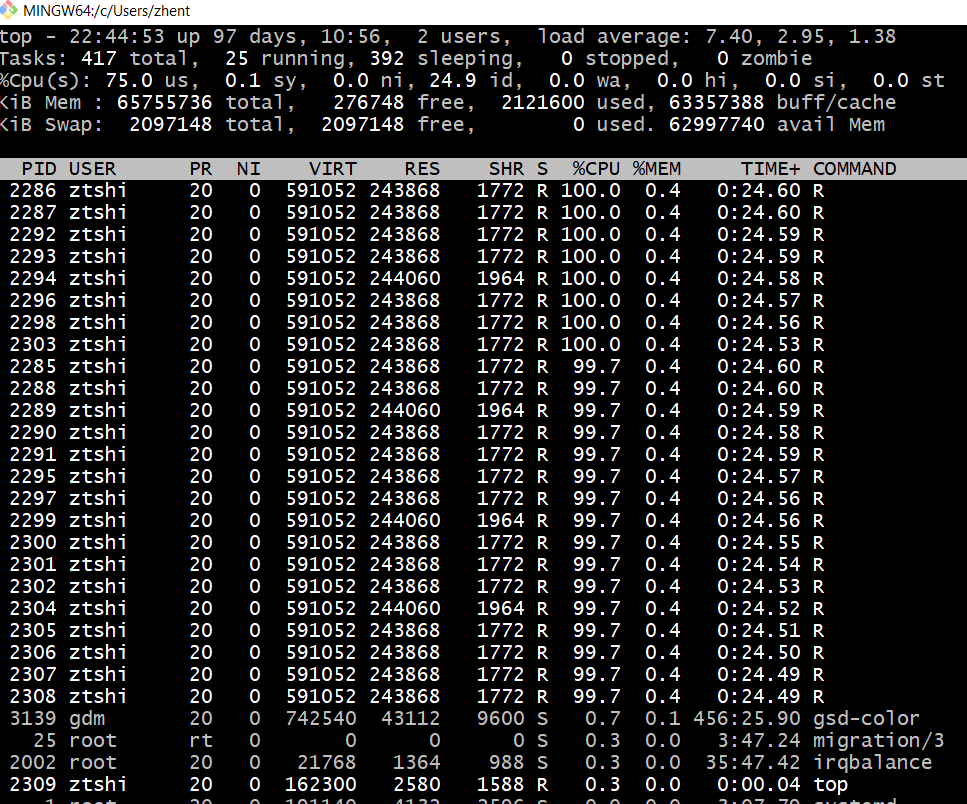
Our department’s computation infrastructure has been improving. A server dedicated to professors is a 32-core machine. Students also have access to a powerful multi-core computer.

\begin{figure} \centering \includegraphics[width = 15cm]{graph/econ_super} \caption{Log into \texttt{econsuper} and check CPU with \texttt{lscpu} } \end{figure}

Log in econsuper.econ.cuhk.edu.hk;
Upload R scripts and data to the server;
In a shell, run R --vanilla <file_name.R> result_file_name.out;
To run a command in the background, add & at the end of the above command.

This example comes from @lin2020. As a demonstration, we only use 15% of the data and a sparse grid of tuning parameters. It makes about 9 minutes with 24 cores.

ssh ztshi@econsuper.econ.cuhk.edu.hk
cd data_example
R --vanilla <Beijing_housing_gbm.R> GBM_BJ.out & 

econ_super

RStudio Server¶

The command line shells lack a graphic interface for interactive data analysis. RStudio server offers a local-like environment via a web browser to communicate with a remote server. The remote server can be specified for users’ need.

RStudio Cloud is a free service to facilitate teaching and demonstration. The underlying computation unit is too weak to execute serious tasks.
Econsuper is our department’s service, which resembles a workplace environment in a small company. We can contact the technicians for our needs. The service is always online (with VPN connection), and much more powerful than the best local computer we can afford.
Amazon Web Service Cloud is commercial service that can be tailored according to one’s budget, from tiny demonstrative display to big enterprise business applications.

AWS

Graphics¶

An English cliché says “One picture is worth ten thousand words”. John Tukey, a renowned mathematical statistician, was one of the pioneers of statistical graphs in the computer era. Nowadays, powerful software is able to produce dazzling statistical graphs, sometimes web-based and interactive. Outside of academia, journalism hooks a wide readership with professional data-based graphs. New York Times and The Economists are first-rate examples; South China Morning Post sometimes also does a respectable job. A well designed statistical graph can deliver an intuitive and powerful message. I consider graph prior to table when writing a research report or an academic paper. Graph is lively and engaging. Table is tedious and boring.

We have seen an example of R graph in the OLS regression linear example in Lecture 1. plot is a generic command for graphs, and is the default R graphic engine. It is capable of producing preliminary statistical graphs.

Over the years, developers all over the world have had many proposals for more sophisticated statistical graphs. Hadley Wickham’s ggplot2 is among the most successful.

ggplot2 is an advanced graphic system that generates high-quality statistical graphs. It is not possible to cover it in a lecture. Fortunately, the author wrote a comprehensive reference ggplot2 book, which can be downloaded via the CUHK campus network (VPN needed).

ggplot2 accommodates data frames of a particular format. reshape2 is a package that helps prepare the data frames for ggplot2.

The workflow of ggplot is to add the elements in a graph one by one, and then print out the graph all together. In contrast, plot draws the main graph at first, and then adds the supplementary elements later.

ggplot2 is particularly good at drawing multiple graphs, either of the same pattern or of different patterns. Multiple subgraphs convey rich information and easy comparison.

Example

Plot the density of two estimators under three different data generating processes. This is an example to generate subgraphs of the same pattern.

load("data_example/big150.Rdata")
library(ggplot2)
library(reshape2)

big150_1 <- big150[, c("typb", "b1", "b1_c")]
print(head(big150_1))

big150_1 <- melt(big150_1, id.vars = "typb", measure.vars = c("b1", "b1_c"))
names(big150_1)[2] <- c("estimator")
print(head(big150_1))

p1 <- ggplot(big150_1)
p1 <- p1 + geom_area(
  stat = "density", alpha = .25,
  aes(x = value, fill = estimator), position = "identity"
)
p1 <- p1 + facet_grid(. ~ typb)
p1 <- p1 + geom_vline(xintercept = 0)
p1 <- p1 + theme_bw()
p1 <- p1 + theme(
  strip.text = element_text(size = 12),
  axis.text = element_text(size = 12)
)
print(p1)

The function ggplot specifies which dataset to use for the graph. geom_*** determines the shape to draw, for example scatter dots, lines, curves or areas. theme is to tune the supplementary elements like the background, the size and font of the axis text and so on.

Example

This example aligns two graphs of different patterns in one page. Similar graphs appear in @shi2018structural.

# graph packages
library(lattice)
library(ggplot2)
library(reshape2)
library(gridExtra)

load("data_example/multigraph.Rdata") # load data


# unify the theme in the two graphs
theme1 <- theme_bw() + theme(
  axis.title.x = element_blank(),
  strip.text = element_text(size = 12),
  axis.text = element_text(size = 12),
  legend.position = "bottom", legend.title = element_blank()
)

# sub-graph 1
d1 <- data.frame(month = 1:480, m = m_vec)
p1 <- qplot(x = month, y = m, data = d1, geom = "line")
p1 <- p1 + theme1 + ylab("fraction of chartists")


# sug-graph 2
d2$month <- 1:480
p2 <- ggplot(d2)
p2 <- p2 + geom_line(aes(x = month, y = value, col = variable))
p2 <- p2 + theme1 + ylab("price and fundamental")

# generate the grahp
grid.arrange(p1, p2, nrow = 2)

In order to unify the theme of the two distinctive subgraphs, we define an object theme1 and apply it in both graphic objects p1 and p2.

Interactive Graph¶

In the folder of data_example, we give a preliminary example of flexdashboard. It is very easy to convert a ggplot2 graph into an HTML interactive graph by plotly::ggplotly().

A Primer on Economic Data Science

Advanced R

Contents

Advanced R¶

Introduction¶

Vectorization¶

Efficient Loop¶

Parallel Computing¶

Cloud Computing¶

Command Line¶

RStudio Server¶

Graphics¶

Interactive Graph¶

Future writing plan¶

Reading¶

References¶